KESEBANGUNAN

●●●● PENGERTIAN KESEBANGUNAN ●●●●

Pernahkah kalian berkunjung ke Tugu Monumen Nasional (Monas) yang ada di Jakarta? Tahukah kalian berapa tinggi monumen tersebut?

                                                      Sumber gambar : deviantart.com
       Untuk mengetahui tinggi monumen tersebut, kalian tidak perlu mengukurnya secara langsung. Akan sangat susah bukan mengukur monumen setinggi itu? Kalian cukup memanfaatkan konsep perbandingan pada foto bersakala yang telah kalian pelajari pada topik sebelumnya. Misalkan objek yang digunakan adalah foto tugu monas dan foto orang yang ada di dekatnya. Dengan mengetahui ukuran tinggi monas dan tinggi orang dalam foto, serta ukuran sebenarnya dari orang yang ada dalam foto, kita akan mengetahui tinggi sebenarnya dari tugu monas tersebut. Lantas, bagaimana caranya jika kita sedang berdiri di dekat tugu monas tanpa sebuah foto? Adakah cara lain yang dapat dilakukan untuk menentukan tingginya? Tentu saja ada. Kalian dapat menggunakan konsep kesebangunan dengan memanfaatkan tinggi bayangan monas dan bayangan kalian. Bagaimana caranya? Mari kita pelajari bersama.

Dua buah bangun dikatakan sebangun jika kedua bangun tersebut memiliki bentuk yang sama dengan ukuran yang bisa sama ataupun berbeda. Cara penulisan bangun-bangun yang sebangun yaitu dengan menggunakan simbol “~”, misalnya bangun PQRS sebangun dengan bangun KLMN, maka ditulis PQRS ~ KLMN. Sekarang, coba perhatikan sekelilingmu. Dapatkah kamu menyebutkan benda-benda yang sebangun? Ya, foto dengan pigura merupakan salah satu contohnya.
Perhatikan gambar persegi panjang berikut:

Apakah persegipanjang ABCD sebangun dengan persegipanjang KLMN?
       Persegipanjang ABCD dan KLMN sebangun karena mereka mempunyai bentuk yang sama, meskipun dengan ukuran yang berbeda. Berdasarkan pengamatan dari kedua bangun tersebut, diketahui bahwa:

• sudut-sudut yang bersesuaian sama besar, yaitu setiap sudut besarnya 90°
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

Perbandingan sisi-sisi kedua persegipanjang tersebut dapat dituliskan sebagai berikut.
ABKL=420=15
BCLM=315=15
DCNM=420=15
DANK=315=15
Dengan demikian, diperoleh hubungan antara sisi-sisi kedua bangun tersebut, yaitu:
ABKL=BCLM=DCNM=DANK
Dari uraian di atas dapat diketahui bahwa dua bangun dikatakan sebangun, jika memenuhi syarat berikut:

Syarat Kesebangunan

• sudut-sudut yang bersesuaian sama besar
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

       Oleh karena dua bangun dikatakan sebangun apabila sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai, maka kita dapat menghitung panjang salah satu sisi yang belum diketahui dengan menggunakan konsep perbandingan seperti pada contoh berikut ini.

Contoh

Contoh 1:

Apakah masing-masing pasangan bangun di bawah ini sebangun?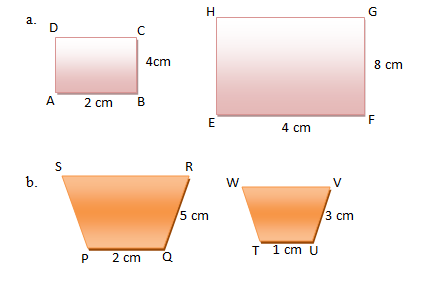

Penyelesaian:

Dua bangun dikatakan sebangun jika:

• sudut – sudut yang bersesuaian sama besar
• sisi-sisi yang bersesuaian mempunyai perbandingan yang senilai

a. Oleh karena kedua bangun tersebut mempunyai bentuk yang sama, yaitu persegipanjang, maka sudut yang bersesuaian sama besar, yaitu 90°, dan sisi-sisi yang bersesuaian adalah:
ABEF=24=12
BCFG=48=12
Terlihat bahwa sisi-sisi yang bersesuaian sebanding.
Jadi, dapat disimpulkan bahwa ABCD dan EFGH adalah dua bangun yang sebangun.
b. Oleh karena kedua bangun tersebut mempunyai bentuk yang sama, yaitu trapesium, maka sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian adalah:
PQTU=21
RQVU=53
Oleh karena sisi-sisi yang bersesuaian tidak sebanding, maka bangun PQRS dan TUVW adalah dua bangun yang tidak sebangun.

Contoh 2:

Perhatikan gambar berikut:

Trapesium ABCD dan PQRS sebangun, tentukanlah:
a. Panjang BC
b. Panjang RS

Penyelesaian:

Perbandingan sisi-sisi yang bersesuaian adalah:
ABPQ=69=23
a. BCQR=ABPQ
⇔BC12=23
⇔BC=23×12=8cm
Jadi, panjang BC adalah 8 cm.
b. CDRS=ABPQ
⇔10RS=23
⇔RS=32×10=15cm
Jadi, panjang RS adalah 15 cm.

Sumber : Quipper School Matematika